
Newton's Beweis des Brechungsgesetzes aufgrund seiner Teilchenvorstellung
kursive Originaltexte aus: Isaac Newton, Optik; Anmerkungen von Gunter Lind
Prop. VI. Lehrsatz 5
Der Sinus des Einfalls steht bei jedem für sich betrachteten Strahle in einem gegebenen Verhältnisse zum Sinus der Brechung.
Aus dem bisher Gesagten ist zur Genüge klar, daß jeder Strahl für sich einen gewissen konstanten Grad der Brechbarkeit besitzt. Die durch die erste Brechung bei gleichem Einfall am stärksten gebrochenen Strahlen werden auch bei den folgenden Brechungen unter gleichem Einfall am stärksten gebrochen, und ebenso die am wenigsten brechbaren und die übrigen, die einen mittleren Grad von Brechbarkeit besitzen, ... Diejenigen aber, die bei gleichem Einfalle das erste Mal gleich gebrochen werden, werden auch nachher gleich und gleichförmig gebrochen, mögen sie ... vor ihrer Trennung voneinander, oder ... einzeln gebrochen werden. Die Brechung jedes einzelnen Strahles ist also eine regelmäßige, und wir wollten jetzt zeigen, welche Regeln diese Brechung befolgt.
Die neueren Schriftsteller über Optik lehren, daß die Sinus des Einfalls zu den Sinus der Brechung in gegebenem Verhältnis stehen ..., und einige, die dieses Verhältnis mit Instrumenten zur Messung der Brechung oder durch sonstige Versuche geprüft haben, sagen, sie hätten dieses Verhältnis ganz genau gefunden. Da sie aber die verschiedene Brechbarkeit der verschiedenen Strahlen nicht kennen und meinen, sie würden sämtlich nach einem und demselben Verhältnis gebrochen, so ist anzunehmen, daß sie ihre Messungen nur auf die mittleren Strahlen des gebrochenen Lichts erstreckt haben, so daß wir aus ihren Messungen nur schließen können, daß die Strahlen, die einen mittleren Grad von Brechbarkeit besitzen, d.h. die ohne die übrigen grün erscheinen, nach einem gegebenen Verhältnis der Sinus gebrochen werden. Deshalb haben wir jetzt zu zeigen, daß ähnliche gegebene Verhältnisse bei den übrigen herrschen. Es ist ja sehr glaublich, daß sich dies so verhält, da die Natur immer gleichförmige Gesetze beobachtet, aber dennoch ist ein experimenteller Nachweis wünschenswert. Einen solchen Beweis werden wir haben, wenn wir zeigen können, daß die Sinus der Brechung der verschiedenen brechbaren Strahlen zueinander in gegebenem Verhältnis stehen, wenn die zugehörigen Sinus des Einfalls einander gleich sind. Denn wenn die Sinus der Brechung aller Strahlen in gegebenem Verhältnis zu dem Sinus der Brechung eines Strahles von einem mittleren Grade der Brechbarkeit stehen, und wenn dieser Sinus zu dem Sinus des gleichen Einfalls in gegebenem Verhältnis steht, so werden die anderen Brechungssinus zu dem gleichen Sinus des Einfalls ebenfalls in gegebenem Verhältnis stehen. Wenn nun die Sinus des Einfalls einander gleich sind, so stehen, wie durch den folgenden Versuch klar werden wird, die Sinus der Brechung untereinander in gegebenem Verhältnis.
In moderner Formelschreibung drückt sich NEWTONs Gedankengang folgendermaßen aus. Er will experimentell zeigen, daß für zwei beliebige Strahlen (1) und (2) gilt:
Da (1) ein beliebiger Strahl ist, kann dafür auch der Strahl mittlerer Brechbarkeit (m) gewählt werden:
Für diesen Strahl gilt aber das Brechungsgesetz
Aus beiden Beziehungen folgt:
Nachdem der Lehrsatz 5 mittels der analytischen Methode festgestellt wurde, geht NEWTON nun daran, ihn mittels der synthetischen Methode zu beweisen.
Soweit es also durch den Versuch den Anschein gewinnt, bestätigt sich das Verhältnis für jeden Strahl besonders; daß dies aber genau richtig ist, kann bewiesen werden auf Grund der Annahme, daß die Körper das Licht brechen, indem sie auf dessen Strahlen in geraden Linien, die auf ihrer Oberfläche senkrecht stehen, einwirken. Zum Zwecke jenes Beweises aber muß man die Bewegung jedes Strahles in zwei Bewegungen zerlegen, eine zur brechenden Fläche senkrechte und eine zu ihr parallele, und muß für die senkrechte Bewegung den folgenden Satz aufstellen.
Wenn eine Bewegung oder irgend ein Bewegtes mit irgendeiner Geschwindigkeit auf einen breiten und dünnen Körper trifft, der beiderseits durch parallele Ebenen begrenzt wird, und beim Durchgang durch denselben von einer Kraft, die in gegebenen Entfernungen von der Ebene eine gegebene Größe besitzt, senkrecht gegen die entferntere Ebene getrieben wird, so wird die senkrechte Geschwindigkeit dieses Bewegten beim Austritte aus dem Körper immer gleich sein der Quadratwurzel aus der Summe des Quadrats der senkrechten Geschwindigkeit beim Auftreffen auf den Körper und des Quadrats derjenigen senkrechten Geschwindigkeit, die er beim Austritte dann haben würde, wenn beim Eintritte die senkrechte Geschwindigkeit unendlich klein wäre. Derselbe Satz bestätigt sich bei einer Bewegung, die beim Durchgange durch den Körper eine senkrechte Verzögerung erfährt, wenn man nur statt der Summe der beiden Quadrate ihre Differenz nimmt. Mathematiker werden den Beweis leichter finden; deshalb will ich den Leser nicht damit behelligen.
Der Satz, den NEWTON hier ohne Beweis angibt, macht eine Aussage über die Geschwindigkeit bei einer gleichförmig beschleunigten Bewegung. NEWTON hatte dieses Thema in seinem Buch "Philosophiae naturalis principia mathematica" behandelt. Den Beweis kann man folgendermaßen führen:
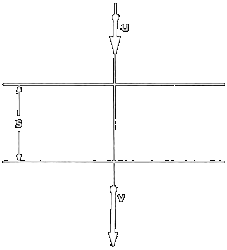 Der Körper trete mit der Geschwindigkeit u in die Schicht der Dicke s ein
und verlasse sie mit der Geschwindigkeit v. Innerhalb von s wirke eine konstante
Kraft in Bewegungsrichtung auf den Körper und vermittle ihm eine konstante
Beschleunigung a. Wenn der Körper zur Zeit t = 0 in die Schicht eintritt,
gilt nach dem Weg-Zeit-Gesetz der gleichförmig beschleunigten Bewegung:
Der Körper trete mit der Geschwindigkeit u in die Schicht der Dicke s ein
und verlasse sie mit der Geschwindigkeit v. Innerhalb von s wirke eine konstante
Kraft in Bewegungsrichtung auf den Körper und vermittle ihm eine konstante
Beschleunigung a. Wenn der Körper zur Zeit t = 0 in die Schicht eintritt,
gilt nach dem Weg-Zeit-Gesetz der gleichförmig beschleunigten Bewegung:
Durch Differenzieren erhält man
Setzt man dies in das Weg-Zeit-Gesetz ein, so ergibt sich:
In dem Sonderfall u
Damit erhält man die von NEWTON angegebene Beziehung
Mit Hilfe dieser Beziehung führt NEWTON seinen Beweis des Sinusgesetzes. Der Beweis zerfällt in zwei Teile. Zum einen wird der Sonderfall des streifend einfallenden Lichts betrachtet und mit seiner Hilfe v0 bestimmt. Sodann wird der Beweis am allgemeinen Fall geführt.
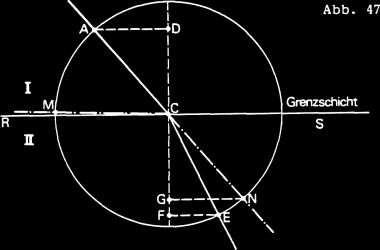 Angenommen, ein sehr schief in der Richtung MC /Abb. 47/ einfallender Strahl
werde bei C durch die Ebene RS nach der Linie CN gebrochen, und es sei verlangt,
die Linie CE zu finden, nach welcher ein anderer Strahl AC gebrochen wird,
so seien MC, AD die Einfallssinus der beiden Strahlen und NG, EF die Sinus
ihrer Brechung; die gleichen Bewegungen der einfallenden Strahlen seien
durch die gleichen Linien MC und AC dargestellt, und während die Bewegung
MC als parallel der brechenden Ebene betrachtet wird, sei die andere Bewegung
AC in die zwei Bewegungen AD und DC zerlegt, von denen AD parallel, DC senkrecht
zur brechenden Fläche RS ist. Ebenso seien die Bewegungen der austretenden
Strahlen in zwei zerlegt, von denen die senkrechten
Angenommen, ein sehr schief in der Richtung MC /Abb. 47/ einfallender Strahl
werde bei C durch die Ebene RS nach der Linie CN gebrochen, und es sei verlangt,
die Linie CE zu finden, nach welcher ein anderer Strahl AC gebrochen wird,
so seien MC, AD die Einfallssinus der beiden Strahlen und NG, EF die Sinus
ihrer Brechung; die gleichen Bewegungen der einfallenden Strahlen seien
durch die gleichen Linien MC und AC dargestellt, und während die Bewegung
MC als parallel der brechenden Ebene betrachtet wird, sei die andere Bewegung
AC in die zwei Bewegungen AD und DC zerlegt, von denen AD parallel, DC senkrecht
zur brechenden Fläche RS ist. Ebenso seien die Bewegungen der austretenden
Strahlen in zwei zerlegt, von denen die senkrechten ![]() und
und ![]() sind.
sind.
An der Grenzschicht RS ändert sich die Geschwindigkeit (oder, wie NEWTON sagt, die Bewegung) des Strahls. Im Medium I stellen die Längen der Radien MC und AC des Einheitskreises der Abb. 47 zugleich die Größe der Lichtgeschwindigkeit dar. Im Medium II müssen die Radienlängen CE und CN jedoch noch mit einem gewissen "Maßstabsfaktor" m multipliziert werden, um wieder die (geänderte) Lichtgeschwindigkeit zu ergeben. Dieser Faktor ergibt sich aus den parallel zu RS gerichteten Geschwindigkeitskomponenten. Bei streifendem Einfall gilt:
Parallelkomponente in I : MC
Parallelkomponente in II : NG · m
Da sich die Parallelkomponente der Geschwindigkeit bei der Brechung nicht ändern soll (was NEWTON bislang nicht explizit erwähnt hat, jedoch gleich anschließend ausführt), ergibt sich
Und damit wird die senkrechte Geschwindigkeitskomponente im Medium II:
Entsprechend ergibt sich die senkrechte Geschwindigkeitskomponente bei beliebigem Einfallswinkel
Damit sind bereits die Größen u und v bestimmt, die im zweiten Teil des Beweises benötigt werden.
Mag nun die Kraft der brechenden Ebene erst
in dieser Ebene auf die Strahlen zu wirken beginnen, oder ihre Wirkung in
einer gewissen Entfernung auf der einen Seite beginnen, in gewisser Entfernung
auf der anderen Seite aufhören, oder mag sie überall zwischen diesen beiden
Grenzen in einer zur brechenden Ebene senkrechten Richtung wirken, und mögen
die Wirkungen auf die Strahlen in gleichem Abstand von der brechenden Ebene
gleich sein, in verschiedenem Abstände nach einem, beliebigen Verhältnisse
gleich oder ungleich: jedenfalls wird die zu der brechenden Ebene parallele
Bewegung des Strahls durch diese Kraft keine Veränderung erfahren und die
darauf senkrechte nach der Regel des obigen Satzes verändert werden. Schreibt
man daher für die senkrechte Geschwindigkeit des austretenden Strahls CN,
wie oben, ![]() , so wird die senkrechte Geschwindigkeit eines anderen austretenden Strahls
CE, welche
, so wird die senkrechte Geschwindigkeit eines anderen austretenden Strahls
CE, welche ![]() war,
war, ![]() sein. Wenn man diese beiden Ausdrücke quadriert, zu ihnen die gleichen Werte
AD2 und MC2 - CD2 addiert und diese Summen
durch die einander gleichen Summen CF2 + EF2 und CG2
+ NG2 dividiert, so erhält man AD2 : EF2
= MC2 : NG2. Mithin ist AD : EF = MC : NG, d.h. der
Sinus des Einfalls steht zum Sinus der Brechung in einem gegebenen Verhältnis.
sein. Wenn man diese beiden Ausdrücke quadriert, zu ihnen die gleichen Werte
AD2 und MC2 - CD2 addiert und diese Summen
durch die einander gleichen Summen CF2 + EF2 und CG2
+ NG2 dividiert, so erhält man AD2 : EF2
= MC2 : NG2. Mithin ist AD : EF = MC : NG, d.h. der
Sinus des Einfalls steht zum Sinus der Brechung in einem gegebenen Verhältnis.
Da u, v und v0 bestimmt sind, kann man die oben hergeleitete
Beziehung ![]() hinschreiben.
hinschreiben.
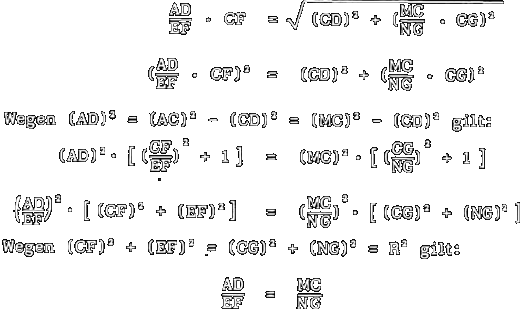
Wenn man den Kreis in Abb. 47 als Einheitskreis auffaßt, gilt:
wobei β0 der Brechungswinkel bei streifendem Einfall ist. Daraus folgt:
NEWTON schließt seinen Beweis mit dem stolzen Satz:
Da dieser Beweis allgemein gilt, gleichviel, worin das Licht bestehen mag oder durch was für eine Kraft es gebrochen wird, ohne irgend eine andere Annahme als die, daß der brechende Körper auf die Strahlen in einer zu seiner Oberfläche senkrechten Richtung einwirke, so betrachte ich dies als einen ganz überzeugenden Beweis für die volle Richtigkeit dieser Proposition.



